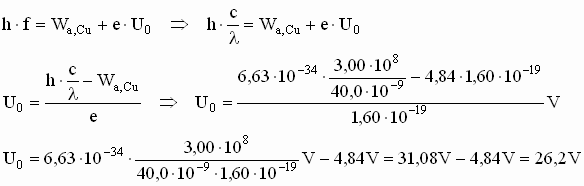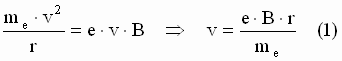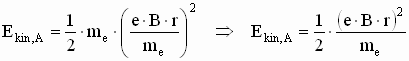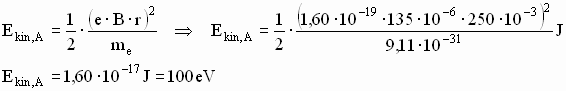Photoeffekt
Die Beobachtungsergebnisse beim äußeren Photoeffekt haben seiner Zeit zu neuen Erkenntnissen über die Natur des Lichts geführt.
|
1. |
Erklären Sie
den äußeren Photoeffekt mit dem Photonenmodell des Lichts. |
|
2. |
Verschiedene
Photokatoden sollen jeweils mit Laserlicht der Wellenlänge λ = 633nm
bestrahlt werden.
1) Barium auf Wolframoxid
|
Aufgaben:
1) Eine Glühlampe
hat eine Leistung von 100W. Wie viele Photonen sendet die Lampe pro Sekunde
aus? (Wirkungsgrad beachten!)
2) Die
Solarkonstante sagt, dass die die Sonne am Ort der Erde ca. 1000 W pro
Quadratmeter an Leistung abgibt.
a) Schätze daraus
die Gesamtleistung der Sonne ab.
b) Schätze wie
viele Photonen die Sonne pro Sekunde emittiert.
Lösung
|
1. |
Tritt ein
Photon der Frequenz f in einen Stoff, z.B. ein Metall ein, so gibt es beim
äußeren Photoeffekt seine ganze Energie an ein Elektron ab, das daraufhin aus
dem Metallverband austritt. Zum Austreten benötigt es bereits einen Teil der
zugeführten Energie, die Austrittsarbeit, den Rest an Energie behält das
Elektron in Form kinetischer Energie. |
|
2. |
|
Lenard-Versuch
1888 bestrahlte W. Hallwachs eine geladene, auf einem Elektroskop
sitzende Metallplatte mit UV-Licht.
|
a) |
Aus welchen
Beobachtungen konnte Hallwachs folgern, dass bei Lichteinstrahlung nur
negative Ladungsträger aus Metallen austreten? (3 BE) |
Bei der skizzierten Vakuumphotozelle zeigt das extrem hochohmige Voltmeter nach dem Einschalten der Beleuchtung die im Diagramm dargestellte zeitabhängige Spannung.

|
b) |
Erklären Sie, wie der dargestellte Spannungsverlauf zustande kommt. (6 BE)
|
|
c) |
Wie verändern sich U0 und die Anfangssteigung der t-U-Kurve, wenn man im Versuch bei gleich bleibender Wellenlänge die Intensität der Bestrahlung erhöht? Begründen Sie kurz Ihre Antwort. (4 BE)
|
|
d) |
Berechnen Sie U0 für eine Kupferplatte, die mit monochromatischem UV-Licht der Wellenlänge λ = 40,0 nm bestrahlt wird. [zur Kontrolle: U0 = 26,2 V] (4 BE)
|
|
Zur
Untersuchung der beim Photoeffekt freigesetzten Elektronen kann man die
nebenstehend skizzierte Lenard-Röhre verwenden. Dabei legt man zwischen die
mit UV-Licht bestrahlte Kathode K und die mit einer Lochblende versehene
Anode A eine variable Spannung U < 1kV. Nach einer weiteren Blende Bl1
gelangen die Elektronen in ein homogenes Magnetfeld der Flussdichte B
senkrecht zur Zeichenebene. Nur die Elektronen, deren Kreisbahn durch die
eingezeichneten Blenden führt, gelangen in einen Metallbecher, der über ein
empfindliches Strommessgerät geerdet ist. |
|
|
e) |
Zeigen Sie,
dass nur solche Elektronen in den Metallbecher gelangen, die beim Eintritt in
das Magnetfeld die kinetische Energie |
Wie in Teilaufgabe 1d sei die Kathode K aus Kupfer und werde mit monochromatischem UV-Licht der Wellenlänge λ = 40,0 nm bestrahlt. Der durch die Versuchsanordnung festgelegte Bahnradius r beträgt 250 mm, die Flussdichte 135 μT.
|
f) |
Zwischen
welchen Grenzen Umin und Umax muss die Spannung U liegen, damit das
Strommessgerät einen von Null verschiedenen Wert anzeigt? |
Lenard-Versuch – Lösung
|
a) |
Bei positiver Aufladung der Metallplatte blieb der Ausschlag des Elektroskops sehr lange unverändert bestehen, bei negativer Aufladung fand dagegen eine rasche Entladung statt, die auf Grund der abstoßenden Kräfte zwischen gleichnamigen Ladungen verständlich ist. Bei positiver Aufladung der Platte konnten sich die Photoelektronen aufgrund der anziehenden elektrischen Kräfte nicht ablösen. |
|
b) |
Ein Teil der aus der Metallplatte ausgelösten Photoelektronen gelangt zur Ringelektrode. Diese wird negativ geladen, die Metallplatte positiv, da der hohe Innenwiderstand des Voltmeters den Ladungsausgleich zwischen Metallplatte und Ringelektrode behindert. Je mehr Elektronen die Ringelektrode erreichen, desto größer wird die Spannung U zwischen Metallplatte und Ringelektrode. Mit zunehmendem U erreichen immer weniger Photoelektronen die Ringelektrode, wodurch U langsamer ansteigt und schließlich einen Maximalwert U0 erreicht, bei dem die schnellsten Photoelektronen die Ringelektrode gerade nicht mehr erreichen.
|
|
c) |
U0 bleibt bei Erhöhung der Bestrahlungsintensität gleich, weil die maximale kinetische Energie der Photoelektronen allein durch die Wellenlänge des eingestrahlten Lichts bestimmt ist. Bei wachsender Bestrahlungsintensität werden pro Zeiteinheit mehr Photoelektronen emittiert, U steigt als schneller an.
|
|
d) |
|
|
e) |
Zentripetalkraft = Lorentzkraft
Für die kinetische Energie der Elektronen bei A gilt:
Setzt man (1) in (2) ein, so ergibt sich:
|
|
f) |
Die minimale Spannung Umin = 74 V, die maximale Spannung Umax = 100 V. Bei kürzerer Wellenlänge des eingestrahlten Lichts ist die maximale kinetische Energie der ausgelösten Photoelektronen größer als 26,2 eV, somit kann die minimale Spannung unter 74 V liegen. Die maximale Spannung ändert sich dadurch nicht, da auch bei kürzerer Wellenlänge einige Elektronen mit vernachlässigbarer Energie auftreten. |
Lenard-Versuch
1888 bestrahlte W. Hallwachs eine geladene, auf einem Elektroskop
sitzende Metallplatte mit UV-Licht.
Bei der skizzierten Vakuumphotozelle zeigt das extrem hochohmige Voltmeter
nach dem Einschalten der Beleuchtung die im Diagramm dargestellte zeitabhängige
Spannung.
|
b) |
Erklären Sie, wie der dargestellte Spannungsverlauf zustande kommt. (6 BE) |
|
c) |
Wie verändern sich U0 und die Anfangssteigung der t-U-Kurve, wenn man im Versuch bei gleich bleibender Wellenlänge die Intensität der Bestrahlung erhöht? Begründen Sie kurz Ihre Antwort. |
Lenard-Versuch
1888 bestrahlte W. Hallwachs eine geladene, auf einem Elektroskop
sitzende Metallplatte mit UV-Licht.
Bei der skizzierten Vakuumphotozelle zeigt das extrem hochohmige Voltmeter
nach dem Einschalten der Beleuchtung die im Diagramm dargestellte zeitabhängige
Spannung.
|
b) |
Erklären Sie, wie der dargestellte Spannungsverlauf zustande kommt. (6 BE) |
|
c) |
Wie verändern sich U0 und die Anfangssteigung der t-U-Kurve, wenn man im Versuch bei gleich bleibender Wellenlänge die Intensität der Bestrahlung erhöht? Begründen Sie kurz Ihre Antwort. |
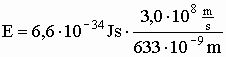 => E = 3,12·10-19 J =1,95 eV
=> E = 3,12·10-19 J =1,95 eV
 besitzen.
(5 BE)
besitzen.
(5 BE)